Arhive autor: Mihail
No, The Laws Of Physics Are Not The Same Forwards And Backwards In Time
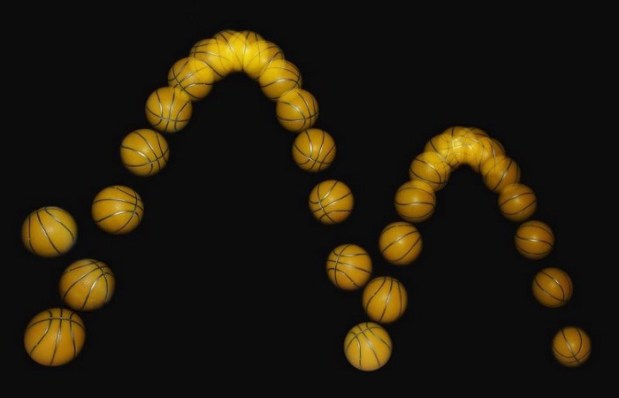
A ball in mid-bounce has its past and future trajectories determined by the laws of physics, but time will only flow into the future for us. While Newton’s laws of motion are the same whether you run the clock forwards or backwards in time, not all of the rules of physics behave identically if you run the clock forwards or backwards. (WIKIMEDIA COMMONS USERS MICHAELMAGGS AND (EDITED BY) RICHARD BARTZ)
No matter when, where, or what you are in the Universe, you experience time in only one direction: forwards. In our everyday experiences, clocks never run backwards; scrambled eggs never uncook and unscramble themselves; shattered glass never spontaneously reassembles itself. But if you were to look at the laws of physics that govern the way the Universe works — from Newton’s laws of motion down to the quantum physics of subatomic particles — you’d find something peculiar and unexpected: the rules are exactly the same whether time runs forwards or backwards.
This corresponds to a certain symmetry of nature: T-symmetry, or time-reversal invariance. Our everyday experience indicates to us, quite strongly, that the laws of physics must violate this symmetry, but for decades, we couldn’t demonstrate it. But a few years ago, we experimentally proved the laws of physics are different depending on which direction time runs. Here’s how we know.

Imagine you and a friend decide to go to Pisa, with one of you standing atop the famous leaning tower and the other located down at the bottom. From the top, whoever throws a ball off the edge can easily predict where it will land down on the bottom. Yet if the person at the bottom were to throw the ball upwards with an equal-and-opposite velocity to the ball that just landed, it would arrive exactly at the location where the person at the top threw their ball from.
This is a situation where time-reversal invariance holds: where the T-symmetry is unbroken. Time reversal can be thought of the same way as motion reversal: if the rules are the same whether you run the clock forwards or backwards, there’s true T-symmetry. But if the rules are different when the clock runs backwards from when the clock runs forwards, the T-symmetry must be broken.

There are two very, very good (but indirect) reasons to believe that T-symmetry must be broken at some deep, fundamental level. The first is a proven theorem known as the CPT theorem. If you have a quantum field theory that obeys the rules of relativity — i.e., is Lorentz invariant — that theory must exhibit CPT-symmetry.
There are three symmetries that are both discrete and fundamental in the context of the Standard Model of particle physics:
- C-symmetry, which demands that you replace all particles with their antiparticles,
- P-symmetry, which demands that you replace all particles with their mirror-image reflections, and
- T-symmetry, which demands that you run the laws of physics backwards in time instead of forwards.

The CPT theorem tells us that the combination of all three symmetries must always be preserved. In other words, a spinning particle moving forwards in time must obey the same rules as its antiparticle spinning in the opposite direction moving backwards in time. If C-symmetry is violated, then PT-symmetry must also be violated by an equal amount to keep the combination conserved. As CP-symmetry violation has already been observed (dating back to 1964), we know that T-symmetry must be violated as well.
The second reason is that we live in a Universe where there’s more matter than antimatter, but the laws of physics we know are completely symmetric between matter and antimatter.

It’s true that there must necessarily be additional physics to what we’ve observed to explain this asymmetry, but there are significant restrictions on the types of new physics that can cause it. They were elucidated by Andrei Sakharov in 1967, who noted:
- The Universe must be in an out-of-equilibrium state.
- Both C-symmetry and CP-symmetry must be violated.
- And baryon number-violating interactions must occur.
Even if we hadn’t observed CP-violating interactions directly, we’d have known that they must occur in order to create a Universe that’s consistent with what we observe. And therefore, since again T-violation is necessarily implied by CP-violation, T-symmetry cannot always hold true.

But there’s an enormous difference, in any science, between either theoretical or indirect evidence for a phenomenon and a direct observation or measurement of the desired effect. Even in instances where you know what the outcome must be, experimental verification must be demanded, or we run the risk of fooling ourselves.
This is true in any area of physics. Sure, we knew by watching the timing of binary pulsars that their orbits were decaying, but only with the direct detection of gravitational waves could we be certain that’s how the energy was being carried away. We knew that event horizons must exist around black holes, but only by directly imaging them did we confirm this prediction of theoretical physics. And we knew that the Higgs boson must exist to make the Standard Model consistent, but only by discovering its unambiguous signatures at the LHC did we confirm it.

In order to directly, experimentally confirm the existence of T-violation, scientists had to be incredibly clever. What one must do is design an experiment where the laws of physics could be directly tested for differences between an experiment that runs forwards in time versus one that runs backwards. And since — in the real world — time only runs forwards, this required some truly creative thinking.
The way to think about this is to remember how entangled quantum states work. If you have two quantum particles that are entangled with one another, you know something about their combined properties, but their individual properties are indeterminate until you make a measurement. Measuring the quantum state of one particle will give you some information about the other one, and will give it to you instantaneously, but you cannot know anything about either individual particle until that critical measurement occurs.

Typically, when we think about quantum entanglement of two particles, we perform experiments involving stable particles, like photons or electrons. But there’s only one type of physics process where CP-violation is known to occur: through decays that proceed through the weak nuclear interaction. In fact, this direct type of CP-violation was observed in 1999, and by the CPT theorem, T-violation must occur. Therefore, if we want to test for direct violation of time reversal symmetry, we’d have to create particles where T-violation occurs, which means creating either baryons or mesons (unstable composite particles) that decay via the weak interactions.
These two properties, of quantum indeterminism and of a decay through the weak interactions, can be leveraged to design the exact type of experiment required to test for the direct violation of T-symmetry.

The way to go about testing time reversal violation directly first proposed only recently, as the technology to produce large numbers of particles that contain bottom (b) quarks has only come about in the past few years. The ϒ particle (the Greek letter Upsilon) is the classic example of a particle containing bottom quarks, as it’s actually a meson made of a bottom quark and a bottom antiquark pair.
Like most composite particles, there are many different energy states and configurations it can exist in, similar to how the hydrogen atom exhibits a variety of possible energy states for the electron to be in. In particular, it was suggested that the 4s energy state holds some special properties, and might be the best candidate for observing T-symmetry violation directly.

The reason? The ϒ(4s) particle, when you create one, decays into into both a neutral B-meson (with a down quark and an anti-bottom quark) and a neutral anti-B-meson (with a bottom quark and an anti-down quark) about 48% of the time. At an electron-positron collider, you have the freedom to tune your collisions to occur at the exact energy needed to create a ϒ(4s) particle, meaning that you can create enormous numbers of B-mesons and anti-B-mesons for all your particle physics needs.
Each meson, either a B or an anti-B, can decay in a few possible ways. Either you can produce:
- a J/ψ (charm-anticharm) particle and a long-lived Kaon,
- a J/ψ particle and a short-lived Kaon,
- or a charged lepton and other particles.
This is interesting, because the first decay has a known value of CP, the second has a known value for CP that’s opposite to the first, and the third decay identifies whether it’s a B or anti-B by virtue of the sign of the charge on the lepton. (A positively-charged anti-lepton indicates a B decay; a negatively-charged lepton indicates an anti-B decay.)

When one member of the B/anti-B pair decays into a J/ψ and a Kaon and the other member decays into a lepton, this gives us the opportunity to test for time-reversal violation. Because these two particles, the B and the anti-B, are both unstable, their decay times are only known in terms of their half-lives: decays don’t occur all at once, but at random times with a known probability.
Then, you’ll want to make the following measurements:
- If the first meson to decay does so into a positively charged lepton, you know that the second must be an anti-B particle.
- You then measure the decay of the anti-B particle, and see how many of them give you a decay into a short-lived Kaon.
- Then, you look for events where the order of decays is reversed and the initial and final states are exchanged, i.e., where the first meson decays into a long-lived Kaon and is followed by the second one decaying into a negatively-charged lepton.
This is a direct test of time-reversal violation. If the two event rates are unequal, the T-symmetry is broken.

It took the creation of over 400 million ϒ(4s) particles to detect time-reversal violation directly, and this was accomplished by the BaBar collaboration back in 2012. The test for the reversal of initial and final entangled states is, to date, the only direct test ever performed to see if T-symmetry is conserved or violated in a direct fashion. Just as anticipated, the weak interactions violate this T-symmetry, proving that the laws of physics are not identical whether time runs forwards or backwards.
In particle physics, the gold standard for experimental significance is a threshold of 5-sigma. Yet BaBar physicists achieved a significance of 14-sigma: a remarkable accomplishment. The reason you’ve likely never heard about it? It was overshadowed by slightly bigger particle physics news occurring in the same year: the discovery of the Higgs boson. But this result maybe Nobel-worthy, too. The laws of nature are not the same forwards and backwards in time. After seven years, it’s time the world felt the impact of this discovery.

Indiferent când, unde, sau ce vă existați în Univers, veți experimenta timpul într-o singură direcție: înainte. În experiențele noastre de zi cu zi, ceasurile nu merg niciodată înapoi; ouăle din omletă nu se desprind și se recompun; sticla sparta nu se reasamblează spontan. Dar dacă ar trebui să te uiți la legile fizicii care guvernează modul în care funcționează Universul – din legile lui Newton de mișcare până la fizica cuantică a particulelor subatomice – vei găsi ceva ciudat și neașteptat: regulile sunt exact la fel dacă timpul curge înainte sau înapoi.
Aceasta corespunde unei anumite simetrii a naturii: simetria T sau invarianța de inversare a timpului. Experiența noastră de zi cu zi ne indică, destul de puternic, că legile fizicii trebuie să încalce această simetrie, dar de zeci de ani nu am putut demonstra acest lucru. Dar, cu câțiva ani în urmă, am demonstrat experimental că legile fizicii sunt diferite în funcție de ce direcție se petrece timpul. Iată cum știm.
Foto-Potrivit legendei, primul experiment care arată că toate obiectele au căzut la aceeași rată, indiferent de masă, a fost realizat de Galileo Galilei din vârful Turnului Înclinat din Pisa. Oricare două obiecte care au căzut într-un câmp gravitațional, în absența (sau neglijarea) rezistenței la aer, vor accelera până la sol la aceeași rată. Acest lucru a fost ulterior codificat ca parte a investigațiilor lui Newton în materie. O minge a coborât din turn și o minge aruncată de pe fundul turnului ar putea avea aceeași traiectorie, așa cum legile mișcării sunt aceleași indiferent de direcția în care curge timpul. (IMAGINI GETTY)
Imaginați-vă că împreună cu un prieten decideți să mergeți la Pisa, iar unul dintre voi este aflat pe vârful celebrului turn înclinat, iar celălalt jos. Din partea de sus, oricine aruncă o minge de la margine poate prezice cu ușurință unde va ajunge jos. Cu toate acestea, dacă persoana de jos ar arunca mingea în sus cu o viteză egală și opusă mingii care tocmai a aterizat, ar ajunge exact la locul în care persoana de la vârf a aruncat mingea.
Aceasta este o situație în care invarianța de inversare a timpului se află: unde simetria T este neîntreruptă. Inversarea timpului poate fi gândită în același mod ca inversarea mișcării: dacă regulile sunt aceleași, indiferent dacă rulați ceasul înainte sau înapoi, există adevărată simetrie T. Dar dacă regulile sunt diferite atunci când ceasul rulează înapoi din momentul în care ceasul rulează înainte, simetria T trebuie să fie întreruptă.
Foto – Diferite cadre de referință, inclusiv poziții și mișcări diferite, unde se pot vedea diferite legi ale fizicii (și ar fi de acord cu privire la realitate) dacă o teorie nu este invariabil relativistă. Faptul că avem o simetrie sub „amplificări” sau transformări de viteză ne spune că avem o cantitate conservată: impuls liniar. Faptul că o teorie este invariantă sub orice formă de transformare de coordonate sau de viteză este cunoscută ca invarianța Lorentz, iar orice simetrie invariantă Lorentz conservă simetria CPT. Cu toate acestea, C, P și T (precum și combinațiile CP, CT și PT) pot fi toate încălcate individual. (WIKIMEDIA COMMONS USER KREA)
Există două motive foarte, foarte bune (dar indirecte) de a crede că simetria T trebuie ruptă la un nivel profund și fundamental. Prima este o teoremă cunoscută ca teorema CPT. Dacă aveți o teorie a câmpului cuantic care respectă regulile relativității – adică este Lorentz invariantă – acea teorie trebuie să prezinte simetria CPT.
Există trei simetrii care sunt atât discrete cât și fundamentale în contextul modelului standard al fizicii particulelor:
C-simetrie, care cere să înlocuiți toate particulele cu antiparticulele lor,
P-simetrie, care cere să înlocuiți toate particulele cu reflecțiile lor de oglindă-imagine, și
T-simetrie, care cere ca tu să conduci legile fizicii înapoi în timp, în loc de înainte.
Foto-Schimbarea particulelor pentru antiparticule și reflectarea acestora într-o oglindă reprezintă simultan simetria CP. Dacă dezintegrările anti-oglindă diferă de dezintegrarea normală, CP este încălcată. Simetria de inversare a timpului, cunoscută sub numele de T, trebuie să fie corectată dacă CP este încălcat. Simetriile combinate dintre C, P și T, toate împreună, trebuie să fie conservate conform legilor actuale ale fizicii, cu implicații pentru tipurile de interacțiuni care sunt și nu sunt permise. (E. SIEGEL / DINTRE GALAXIE)
Teorema CPT ne spune că combinația tuturor celor trei simetrii trebuie păstrată întotdeauna. Cu alte cuvinte, o particulă care se rotește înainte în timp trebuie să respecte aceleași reguli ca și antiparticula sa care se rotește în direcția opusă, în mișcare înapoi în timp. Dacă este încălcată simetria C, atunci simetria PT trebuie să fie încălcată cu o sumă egală pentru a menține combinația conservată. Deoarece încălcarea simetriei CP a fost deja observată (datând din 1964), știm că trebuie să fie încălcat și simetria T.
Al doilea motiv este că trăim într-un Univers unde există mai multă problemă decât antimateria, dar legile fizicii pe care le cunoaștem sunt complet simetrice între materie și antimaterie.
Foto-Dacă creați particule noi (cum ar fi X și Y aici) cu omologii, trebuie să conservați CPT, dar nu neapărat C, P, T sau CP singuri. Dacă CP este încălcată, căile de dezintegrare – sau procentul de particule care se distrug într-o direcție față de alta – pot fi diferite pentru particule în comparație cu antiparticulele, ducând la o producție netă de materie peste antimaterie dacă condițiile sunt corecte. (E. SIEGEL / DINTRE GALAXIE)
Este adevărat că trebuie să existe în mod necesar o fizică suplimentară la ceea ce am observat pentru a explica această asimetrie, dar există restricții semnificative asupra tipurilor de fizică nouă care o pot provoca. Ele au fost elucidate de Andrei Saharov în 1967, care a remarcat:
Universul trebuie să fie într-o stare de echilibru.
Atât simetria C cât și simetria CP trebuie încălcate.
Trebuie să se producă interacțiuni care încalcă numărul baryonului.
Chiar dacă nu ar fi observat direct interacțiunile care încalcă CP, am fi știut că trebuie să apară pentru a crea un univers care să fie în concordanță cu ceea ce observăm. Și, prin urmare, din moment ce violarea T este obligatoriu impusă de încălcarea CP, simetria T nu poate fi întotdeauna adevărată.
Foto-Rata decăderii orbitale a unui pulsar binar este în mare măsură dependentă de viteza gravitației și de parametrii orbitali ai sistemului binar. Am folosit date pulsare binare pentru a constrânge viteza gravitației să fie egală cu viteza luminii la o precizie de 99,8% și să deducem existența undelor gravitaționale cu decenii înainte ca LIGO și Fecioara să le detecteze. Cu toate acestea, detectarea directă a undelor gravitationale a fost o parte vitală a procesului științific, iar existența undelor gravitaționale ar fi în continuare îndoieli fără ea. (NASA (L), INSTITUTUL MAX PLANCK PENTRU RADIO ASTRONOMIE / MICHAEL KRAMER (R))
Dar există o diferență enormă, în orice știință, între dovezile teoretice sau indirecte pentru un fenomen și o observație directă sau măsurarea efectului dorit. Chiar și în situațiile în care știi care este rezultatul trebuie să fie cerută verificarea experimentală sau riscul de a ne păcăli pe noi înșine.
Acest lucru este valabil în orice domeniu al fizicii. Desigur, am știut, urmărind momentul în care pulsatorii binari au căzut orbitele lor, dar numai cu detectarea directă a undelor gravitaționale putem fi siguri că energia a fost îndepărtată. Știam că orizonturile evenimentului trebuie să existe în jurul găurilor negre, dar numai prin imaginarea directă a acestora am confirmat această predicție a fizicii teoretice. Și am știut că bosonul Higgs trebuie să existe pentru a face modelul standard consistent, dar numai prin descoperirea semnelor sale lipsite de ambiguitate la LHC am confirmat-o.
Foto-Prima detectare robustă, de 5 sigma a bosonului Higgs, a fost anunțată acum câțiva ani de colaborările CMS și ATLAS. Dar bosonul Higgs nu face un singur „spike” în date, ci mai degrabă o ciocnire împrăștiată, datorită incertitudinii sale inerente în masă. Masa sa de 125 GeV / c² este un puzzle pentru fizica teoretică, dar experimentaliștii nu trebuie să ne îngrijoreze: există, putem să-l creăm și acum putem măsura și studia și proprietățile sale. (COLABORAREA CMS, „OBSERVAREA DECATULUI DIPHOTON AL BOSONULUI HIGGS ȘI MĂSURAREA PROPRIETĂȚILOR SALE”, (2014))
Pentru a confirma direct, experimental existența încălcării T, oamenii de știință trebuiau să fie incredibil de inteligenți. Ceea ce trebuie făcut este să proiectăm un experiment în care legile fizicii ar putea fi testate direct pentru diferențele dintre un experiment care merge mai departe în timp, față de unul care merge înapoi. Și din moment ce – în lumea reală – timpul merge doar înainte, acest lucru necesită o gândire cu adevărat creatoare.
Modul de a ne gândi la acest lucru este să ne amintim cum funcționează statele cuantice încurcate. Dacă aveți două particule cuantice care sunt încurcate unul cu altul, știți ceva despre proprietățile lor combinate, dar proprietățile lor individuale sunt nedeterminate până când faceți o măsurătoare. Măsurarea stării cuantice a unei particule vă va oferi câteva informații despre cealaltă și vă va da instantaneu, dar nu puteți ști nimic despre nici o particulă individuală până când nu are loc măsurarea critică.
Foto-Dacă două particule sunt încurcate, ele au proprietăți funcționale complementare, iar măsurarea determină proprietățile celuilalt. Dacă creați două particule sau sisteme încurcate și măsurați modul în care unul se descompune înaintea celuilalt, ar trebui să puteți măsura reacția în timp inversă pentru a testa conservarea sau încălcarea simetriei T. (WIKIMEDIA COMUNE USER DAVID KORYAGIN)
În mod tipic, când ne gândim la bruiajul cuantic a două particule, efectuăm experimente care implică particule stabile, cum ar fi fotoni sau electroni. Dar există un singur tip de proces fizic în care este cunoscută încălcarea CP: prin descreșteri care se desfășoară prin interacțiunea nucleară slabă. De fapt, acest tip direct de încălcare a CP a fost observat în 1999, iar prin teorema CPT, trebuie să se producă încălcarea T. Prin urmare, dacă vrem să testeze pentru încălcarea directă a simetriei de inversare a timpului, ar trebui să creăm particule în care are loc încălcarea T, ceea ce înseamnă crearea fie a baryonilor, fie a mezonilor (particule compuse instabile) care se distrug prin interacțiunile slabe.
Aceste două proprietăți, de indeterminism cuantic și de o descompunere prin interacțiunile slabe, pot fi utilizate pentru a proiecta exact tipul de experiment necesar pentru a testa încălcarea directă a simetriei T.
Foto-B-mezonii se pot deteriora direct într-o particulă J / Ψ (psi) și o particulă Φ (phi). Oamenii de știință din CDF au descoperit dovezi că unii mezonii B se deteriorează în mod neașteptat într-o structură intermediară tetraquark identificată ca o particulă Y, unde tetraquark constă din două cuarci și două antiquarks. Când un sistem compozit, cum ar fi particula Y, se descompune în două stări care au valori diferite pentru proprietățile CP, ele trebuie să aibă proprietăți diferite și pentru proprietățile T, permițând oamenilor de știință să creeze un experiment care să poată testa direct încălcarea T . (SYMMETRY MAGAZINE)
Modalitatea de a examina încălcarea inversării timpului a fost propusă inițial abia recent, deoarece tehnologia de a produce un număr mare de particule care conțin quarks de jos (b) a avut loc numai în ultimii ani. Partea Y (litera grecească Upsilon) este exemplul clasic al unei particule care conține quark-uri de fund, deoarece este de fapt un mezon alcătuit dintr-un quark de fund și o pereche antiquark de fund.
Ca majoritatea particulelor compozite, există multe stări de energie diferite și configurații în care poate exista, similar cu modul în care atomul de hidrogen prezintă o varietate de stări de energie posibile pentru ca electronul să fie înăuntru. În particular, sa sugerat că starea energiei 4s unele proprietăți speciale și ar putea fi cel mai bun candidat pentru observarea directă a încălcării simetriei T.
Foto-Într-un sistem atomic, each s orbital (red), each of the p orbitals (yellow), the d orbitals (blue) and the f orbitals (green) pot conține numai doi electroni: un spin și un spin în fiecare unu. Într-un sistem nuclear, chiar și într-un mezon care are doar un quark și un antiquark, există orbite similare (și stări energetice). În particular, starea 4s a particulei Upsilon (Υ) are proprietăți deosebit de interesante și a fost creată de sute de milioane de ori pentru colaborarea cu BaBar la SLAC. (LIBRARE LIBRETEXT / NSF / UC DAVIS)
Motivul? Partea Y (4s), atunci când creați una, se descompune atât într-un mezon neutru B (cu un quark jos și un quark anti-jos) și un mezon neutru anti-B (cu un quark de fund și un anti- jos quark) aproximativ 48% din timp. La un collider cu electroni-pozitroni, aveți libertatea de a vă adapta coliziunile la energia exactă necesară pentru a crea o particulă Y (4s), ceea ce înseamnă că puteți crea un număr enorm de mezoni B și mezoni anti-B pentru toți fizica particulelor are nevoie.
Fiecare mezon, fie un B sau un anti-B, se poate descompune în câteva moduri posibile. Fie puteți produce:
o particulă J / ψ (charm-anticharm) și un Kaon cu durată lungă de viață,
o particulă J / ψ și un Kaon de scurtă durată,
sau un lepton încărcat și alte particule.
Acest lucru este interesant, deoarece prima decădere are o valoare cunoscută de CP, cea de-a doua are o valoare cunoscută pentru CP care este opusă primei, iar a treia decădere identifică dacă este B sau anti-B în virtutea semnului de încărcare pe lepton. (Un anti-lepton încărcat pozitiv indică o descompunere B, un lepton încărcat negativ indică o descompunere anti-B).
Foto-O configurare a sistemului utilizat de colaborarea BaBar pentru a verifica direct încălcarea simetriei de inversare a timpului. Partea Y (4s) a fost creată, se descompune în două mezone (care poate fi o combinație B / anti-B) și apoi ambii B și mezonii anti-B se vor deteriora. Dacă legile fizicii nu sunt invariabile în inversarea timpului, diferențele diferite într-o anumită ordine vor prezenta proprietăți diferite. Acest lucru a fost confirmat în 2012. (APS / ALAN STONEBREAKER)
Atunci când un membru al perechii B / anti-B se descompune într-un J / ψ și un Kaon, iar celălalt membru se descompune într-un lepton, acest lucru ne oferă posibilitatea de a testa pentru încălcarea timpului-inversare. Deoarece aceste două particule, B și anti-B, sunt ambele instabile, timpii lor de dezintegrare sunt cunoscuți doar în termenii perioadelor de înjumătățire: dezintegrările nu apar tot o dată, ci în momente aleatorii cu o probabilitate cunoscută.
Apoi, veți dori să efectuați următoarele măsurători:
Dacă primul mezon care se descompune într-un lepton pozitiv încărcat, știți că al doilea trebuie să fie o particulă anti-B.
Apoi măsurați descompunerea particulei anti-B și vedeți câte dintre ele vă dau o descompunere într-un Kaon de scurtă durată.
Apoi, căutați evenimente în care ordinea descompunerilor este inversată și se schimbă stările inițiale și finale, adică unde primul mezon se descompune într-un Kaon cu durată lungă de viață și este urmat de cel de-al doilea care se descompune într-un lepton încărcat negativ.
Acesta este un test direct al încălcării timp-inversare. Dacă cele două rate ale evenimentelor sunt inegale, simetria T este întreruptă.
Foto-Există patru asimetrii independente de inversarea timpului de întârziere în sistemul de degradare Y (4s), corespunzând dezintegrărilor în leptonele încărcate și combinațiile farmec quark-antiquark. Curba albastră punctată reprezintă cea mai bună potrivire a datelor BaBar fără încălcarea T; puteți vedea cât de absurd este rău. Curba roșie reprezintă datele cele mai potrivite cu încălcarea T. Pe baza acestui experiment, încălcarea directă a T este suportată la nivelul de 14 sigmați. (J. P. LEES ET AL. (COLABORAREA BABAR), PHYS. REV. LETT. 109, 211801 (2012))
A fost nevoie de crearea a peste 400 de milioane de particule Y (4s) pentru a detecta direct încălcarea inversă a timpului, iar acest lucru a fost realizat prin colaborarea cu BaBar în 2012. Testul pentru inversarea statelor inițiale și finale este, până în prezent, doar testul direct realizat vreodată pentru a vedea dacă simetria T este conservată sau încălcată în mod direct. Asa cum era de așteptat, interacțiunile slabe încalcă aceasta simetrie T, dovedind ca legile fizicii nu sunt identice dacă timpul merge înainte sau înapoi.
În fizica particulelor, standardul de aur pentru semnificație experimentală este un prag de 5-sigma. Cu toate acestea, fizicienii BaBar au obținut o semnificație de 14-sigma: o realizare remarcabilă. Motivul pentru care probabil nu ați auzit niciodată despre asta? A fost umbrită de știrile despre fizica particulelor ceva mai mari care au avut loc în același an: descoperirea bosonului Higgs. Dar ar putea să se transforme într-un nobil premiu Nobel. Legile naturii nu sunt aceleași înainte și înapoi în timp. După șapte ani, este timpul ca lumea să simtă impactul acestei descoperiri.
***
Imaginea zilei

Imaginea zilei – Cunună de Sânziene

~ Azi mi-am împletit cunună
Din flori mici de Sânziene,
Să fac vrăji la mândra lună
Și descântece-n catrene.
Și-am să spun cuvinte salbă,
Să se ducă pân-la ceruri
Și-oi dansa desculță-n iarbă
Și-oi cânta cântec de doruri.
Și-ai să vii la mine-ndată,
Să-ți dau dragoste de zână
Și n-o să mai pleci vreodată
Doar când ne-o despărți țărâna.
Am să-ți pun iubire-n suflet
Și un dor să nu-l poți ține
Să te usuce până-n creștet
Cum mă uscă el pe mine.
Căci o femeie când iubește,
Cu iubire-adevărată
Nimic nu o oprește
Decât dragostea curată.
Ceapa
Iau virajul spre Sifonăria lui Vasile.
Vasile absent. Îi nevastă-sa.
Îmi piere tot cheful. Nici nu pot să întreb ce-i cu Vasile… La un metru șai’ș’cinși și o sută tri’ dă kile, bașca cam vânăt de la pateu în derivă, devine evident.
− Neața!
− Vasile bolește, mă scutește madama, cu un text prefabricat, de preambulul la care eram temător și mă dezinhibez:
− Da’… ce? O băut din ghinul lui?
O văd că se-negrește așa că salvez in extremis:
− Bagă-un sfert!
Nu știe să pornească rotisorul, nu știe să condimenteze carnea de pui, și-o expediez înapoi la bar gândind cu groază că dihania de Vasile o să dea colțul și, odată cu el, viața mea va lua o cotitură nefastă.
Dar, odată văzute spinările de pui cu aripe boite cu seu de curcan, usturoi zdrobit și presărate cu cimbru și boia iute, trase-n în țeapă, rotindu-se agale, starea mea de spirit revine în parametri: Ce-o fi, om vedea. O viață-avem și-o gaură în cur!
Mă, și-i o vreme de primăvară, aburi se ridică din pământ, așe la vreo nouă’șpe grade și-un soare galeș care se strecoară timid printre nori dând fiori de plăcere, parcă și timpul de montă s-a decalat, prospături egoist încarcerate în brațe protectoare defilează pe bulevard, vacanță…
Intră un familiar:
− Ahoe!
− Salve! îi răspund cu ochii la grill, what’s up?
− Well! Și către patroneasă: bagă-o drojdie și să vă zic ce-am pățit azi noapte.
Madama îl onorează și, după ce soarbe, prețios, din vârful buzelor, amicul continuă:
− Azi noapte, pe la două, numai ce aud niște bubuituri în ușă. Mi s-a săltat tensiunea. La ușă doi polițai, mă, să mi se moaie genunchii, și știți că nu-s slab de înger de felul meu, dar tocmai ce visam niște perversiuni sexuale.
Face o pauză strategică, ca să se recepteze adânc, dar cum vede că noi nu pistonăm, ba de-a dracului eu mă întorc cu spatele ca să ung puișorii cu zeamă, revine mai așezat:
− Da, mă! Doi polițai. Neața! bâigui eu, iar ei mă interpelează cu un ton hotărât: Ceapa!
− Ceee… ceapă? Îmi revine un simț al umorului grotesc, a la Ionesco: ați luat brânză și n-aveți ceapă?
− Noi nu glumim, cetățene, am primit o reclamație cum că un individ fură ceapă de pe spațiul cultivat din spatele blocului. Ne-am deplasat cu celeritate la locul infracțiunii, dar făptașul nu mai era prezent. Totuși, reclamantul va indicat pe dumneavoastră ca fiind prezumtivul delapidator. Avem și mandat de percheziție.
Simt că mă translez într-o lume paralelă, orwelleiană:
− De sunt eu acela, fiți fără de milă! Casa e a voastră: să apară ceapa!
Aveam o teamă, căci aveam niște ceapă în lada cu legume, dar se pare că aveau suficient discernământ încât să decidă că-i veche și luată de la aprozar.
S-au retras spre ușă, dar fără a da semne de abandon:
− Să nu credeți că noi nu am făcut cercetări la locul infracțiunii. Fapta este irefutabilă plimbând pe limbă și accentuând, cu o satisfacție evidentă, ultimul cuvânt agentul mai scund și cu figură porcină.
− Noi ne cerem scuze pentru deranj, dar legea trebuiește aplicată chiar și atunci când, accidental, apar… pare că se gândește intens: dacă ați auzit ceva, sau ceva va atras atenția, noi…
Îmi zic: e timpul tău, Costică!
− Ce să zic… Deasupra… Cam pe la ora zece se auzeau niște zgomote suspecte.
− Aha! exclamă cel scund, care părea și șeful. Hai, Bolovane!
Deasupra stă Tobă. Ne avem bine până când nu mă inundă atunci când uită apa de la cadă deschisă…
În liniștea nopții bocancii polițailor răsunau precum niște salve de tun pe fiecare treaptă pe care călcau spre victima nevinovată. Mi se strânge inima, dar o știu pe procuroare, și-un tanc are ezitări dinaintea ei.
− Și? mă bag în vorbă pentru că amicul părea stânjenit.
− Și… S-au dus la vale vâjâind. I-a spurcat Tamburina de nu-i mai spală zece ape…
− Și?! insist diabolic.
− Și… S-a scoborât la mine. Era ca o fiară…
− Și, și?
− Ce voiai să fac? Ne sărise somnul la amândoi… Ne-am futut până dimineață. Îs ude cearșafurile, mă dor toate alea… Madame?! Mai bag-o drojdie, să-mi vin în fire!!!
***
Imaginea zilei

Space radiation hasn’t contributed to astronaut mortality — yet, study shows
Many aspects of how the human body will react to long periods in space remain unknown. But using the small group of people who have already been there as subjects, researchers are beginning to get some answers.
Robert Reynolds of Mortality Research & Consulting, Inc., in California led a research project published Thursday in Scientific Reports. In it, he and his colleagues used statistical methods to verify that out of the more than 400 astronauts and cosmonauts who had been to space, they could find no linkage between causes of death and damage from radiation. It’s not a reason for future space farers to breathe easy quite yet — after all, they could be in space much longer — but it does offer some reassurance about the levels of radiation human space adventurers have experienced so far.
Causes of Death
The researchers looked at data on 301 astronauts and 117 cosmonauts who had traveled to space between roughly 1960 and 2018 (the data available differed slightly between agencies), looked at how many had died (89 in total) and broke them down by cause of death. This of course weights the sample toward the earlier generations of space farers, as most of the recent astronauts and cosmonauts are still very much alive.
Still, the largest category for cause of death for astronauts was “external,” including spacecraft, aircraft and automobile accidents. A full 38 percent of astronaut deaths could be chalked up to such mishaps, while for cosmonauts, the number was 17 percent.
But the areas the researchers were most interested in were deaths due to cancer or cardiovascular disease, both of which can be linked to radiation damage. For astronauts, the breakdown was 30 percent due to cancer and an additional 15 percent due to cardiovascular disease. For cosmonauts, a full 50 percent of all recorded deaths were due to cardiovascular disease, while another 28 percent were due to cancer.
While those numbers might seem high, it’s worth remembering that cancer and cardiovascular disease in general are common causes of death. What the researchers were looking for was whether they could statistically link the two groups – astronauts and cosmonauts – and the two causes of death – cancer and cardiovascular disease – to an underlying common cause, such as exposure to radiation.
They couldn’t. They found no trend in the deaths suggesting any common cause, meaning radiation didn’t play a major role in the health outcomes of the astronauts and cosmonauts they studied.
Of course, this doesn’t mean humans are in the clear.
“We would expect that at some level of dose there should be adverse health effects,” Reynolds says. “We keep getting the answer ‘no.’ This doesn’t mean radiation isn’t harmful or greater doses wouldn’t be. But so far the doses have been low enough that we don’t see anything.”
That’s probably because the vast majority of space farers so far have spent most or all of their time in Earth orbit, where Earth’s magnetic fields still protect them from the majority of harmful space radiation. Only those 24 astronauts who ventured to the Moon went beyond Earth’s radiation protection, and they stayed for just a few days.
Reynolds says that it’s difficult to draw meaningful results from that tiny sub-sample of people.
By contrast, a Mars mission might last multiple years, and would take place almost entirely beyond Earth’s shielding.
Other researchers are looking at alternative ways of testing the dangers of radiation exposure. But it’s possible that the next round of human space explorers will be guinea pigs, much like the first generation, and only time will tell how radiation has affected them.

O analiză asupra tuturor astronauților și cosmonauților vii și morți arată că radiațiile nu au contribuit în mod semnificativ la ratele lor de mortalitate.
Pe măsură ce NASA și alte agenții se pregătesc să plaseze oamenii pe Lună, Marte și alte destinații mult dincolo de atmosfera Pământului și câmpurile sale magnetice ocrotitoare, cresc și îngrijorările cu privire la radiațiile dăunătoare din spațiu.
Multe aspecte ale modului în care corpul uman va reacționa la perioade lungi în spațiu rămân necunoscute. Dar folosind ca subiecți grupul mic de oameni care au fost deja acolo cercetătorii încep să primească niște răspunsuri.
Robert Reynolds de la Mortality Research & Consulting, Inc., din California, a condus un proiect de cercetare publicat joi în care el și colegii săi au folosit metode statistice pentru a verifica pe cei peste 400 de astronauți și cosmonauți care au fost în spațiu și nu au putut găsi nici o legătură evidentă între cauzele de deces și daunele cauzate de radiații. Nu este un motiv pentru viitorii conchistadori ai spațiului să respire mai ușor – căci, ei ar putea sta în spațiu mult mai mult – dar oferă unele reasigurări cu privire la nivelurile de radiații pe care aventurierii spațiali le-au suportat până acum.
Cauzele morții
Cercetătorii au analizat date despre 301 de astronauți și 117 de cosmonauți care au călătorit în spațiu între aproximativ 1960 și 2018 (datele disponibile diferă ușor între agenții), au analizat câte persoane au murit (89 în total) și le-au separat în funcție de cauza morții . Acest lucru, desigur, în special la pionieri explorării cosmosului, deoarece majoritatea astronauților și cosmonauților de dată recentă sunt încă foarte vii.
Totuși, cea mai mare categorie de cauze de deces pentru astronauți era „externă”, inclusiv nave spațiale, avioane și accidente de automobile. Un procent de 38% din decesele astronauților ar putea fi atribuite unor astfel de neajunsuri, în timp ce pentru cosmonauți, procentul a fost de 17%.
Dar zonele în care cercetătorii au fost cel mai interesați au fost decesele cauzate de cancer sau boli cardiovasculare, ambele putând fi legate de daunele cauzate de radiații. Pentru astronauți, defalcarea a fost de 30% din cauza cancerului și de alte 15% din cauza bolilor cardiovasculare. Pentru cosmonauți, un procent de 50% din totalul deceselor înregistrate se datorează bolilor cardiovasculare, în timp ce alte 28% se datorează cancerului.
În timp ce cifrele ar putea părea ridicate, merită să ne amintim că cancerul și bolile cardiovasculare, din păcate, au devenit cauze comune ale morții. Ceea ce cercetătorii au cautat a fost dacă ar putea să lege statistic cele două grupuri – astronauți și cosmonauți – și cele două cauze de deces – cancer și boli cardiovasculare – la o cauza comună subadiacentă, cum ar fi expunerea la radiații.
Nu au putut. Ei nu au descoperit nici o tendință în decesele care să sugereze orice cauză comună, adică radiațiile nu au jucat un rol major în rezultatele de sănătate ale astronauților și cosmonautului studiați.
Desigur, acest lucru nu înseamnă că oamenii sunt exonerați.
Ne-am aștepta că un anumit nivel de doză de radiații ar trebui sa aibă efecte adverse asupra sănătății, Reynolds spune: „Continuăm să obținem răspunsul nu . Aceasta nu înseamnă că radiația nu este dăunătoare sau că dozele mai mari nu ar fi. Dar până acum dozele de radiații au fost destul de scăzute încât nu vedem nimic. ”
Aceasta este probabil pentru că marea majoritate a pionierilor spațiali au petrecut până acum majoritatea sau tot timpul pe orbita Pământului, unde câmpurile magnetice ale Pământului îi protejează încă de majoritatea radiațiilor spațiale dăunătoare. Doar cei 24 de astronauți care s-au aventurat pe Lună au depășit protecția împotriva radiațiilor a Pământului și au rămas doar câteva zile.
Reynolds spune că este dificil să obțină rezultate semnificative de la acel mic subeșantion de oameni.
Dimpotrivă, o misiune a lui Marte ar putea dura mai mulți ani și ar avea loc aproape în întregime dincolo de ecranarea Pământului.
Alți cercetători se gândesc la modalități alternative de testare a pericolelor expunerii la radiații. Este posibil ca următoarea rundă de exploratori ai spațiului să fie cobai, la fel ca prima generație, și numai timpul va spune cum ia afectat radiația.
***
Something sweet !!!
BLACK HOLES ARE EVEN STRANGER THAN YOU CAN IMAGINE

An artist’s impression of a Sun-like star close to a rapidly spinning supermassive black hole, with a mass of about 100 million times the mass of our Sun. – Image Credit: ESA/Hubble, ESO, M. Kornmesser
Our love of black holes continues to grow as our knowledge of these celestial bodies expands. The latest news is the discovery of a rare “middleweight” black hole, a relative newcomer to the black hole family.
We already knew that some black holes are just a few times the mass of our Sun, while others are more than a billion times as massive. But others with intermediate masses, such as the one 2,200 times the mass of our Sun recently discovered in the star cluster 47 Tucanae, are surprisingly elusive.
So what is it about black holes, these gravitational prisons that trap anything that gets too close to them, that captures the imagination of people of all ages and professions?
‘DARK STARS’
As far back as 1783, within the framework of Newtonian dynamics, the concept of “dark stars” with sufficiently high density that not even light can escape their gravitational pull had been advanced by the English philosopher and mathematician John Michell.
Almost immediately after Albert Einstein presented his theory of general relativity in 1915, which supplanted Newton’s description of our Universe and revealed how space and time are intimately linked, fellow German Karl Schwarzschild and Dutchman Johannes Droste independently derived the new equations for a spherical or point mass.
Although at the time the issue was still something of a mathematical curiosity, over the ensuing quarter of a century nuclear physicists realised that sufficiently massive stars would collapse under their own weight to become these previously theorised black holes.
Their existence was eventually confirmed by astronomers using powerful telescopes, and more recently colliding black holes were the source of the gravitational waves detected with the LIGO instrumentation in the United States.
A DENSE OBJECT
The densities of such objects is mind-boggling. If our Sun were to become a black hole, it would need to collapse from its current size of 1.4 million km across to a radius of less than 3km (6km across). Its average density within this “Schwarzschild radius” would be nearly 20 billion tonnes per cubic centimetre.
The increasing strength and pull of gravity as you get closer to a black hole can be dramatic.
On Earth, the strength of the gravitational pull holding you to its surface is roughly the same at your feet as it is at your head, which is a little bit farther away from the planet.
A video simulation of two black holes merging.
But near some black holes, the difference in gravitational pull from head to toe is so great that you would be pulled apart and stretched out on an atomic level, in a process referred to as spaghettification.
In 1958, the American physicist David Finkelstein was the first to realise the true nature of what has come to be called the “event horizon” of a black hole. He described this boundary around a black hole as the perfect unidirectional membrane.
It’s an intangible surface encapsulating a sphere of no return. Once inside this sphere, the gravitational pull of the black hole is too great to escape – even for light.
In 1963, the New Zealand mathematician Roy Kerr solved the equations for the more realistic rotating black holes. These yielded closed time-like curves that permitted movement backwards through time.
While such strange solutions to the equations of general relativity first appeared in the 1949 work of Austrian-American logician Kurt Gödel, it is commonly thought that they must be a mathematical artefact yet to be explained away.
BLACK AND WHITE HOLES
In 1964, two Americans, the writer Ann Ewing and the theoretical physicist John Wheeler, introduced the term “black hole”. Subsequently, in 1965, the Russian theoretical astrophysicist Igor Novikov introduced the term “white hole” to describe the hypothetical opposite of a black hole.
The argument was that if matter falls into a black hole, then perhaps it is spewed out into our universe from a white hole.
This idea is partly rooted in the mathematical concept known as an Einstein-Rosen bridge. Discovered (mathematically) in 1916 by the Austrian physicist Ludwig Flamm, and re-introduced in 1935 by Einstein and the American-Israeli physicist Nathan Rosen, it was later termed a “wormhole” by Wheeler.
In 1962, Wheeler and the American physicist Robert Fuller explained why such wormholes would be unstable for transporting even a single photon across the same universe.
FACT AND FICTION
Not surprisingly, the idea of entering a (black hole) portal and re-emerging somewhere else in the universe – in space and/or time – has spawned countless science fiction stories, including Doctor Who, Stargate, Fringe, Farscape and Disney’s Black Hole.
Ongoing productions can simply claim that their characters are travelling to a different or a parallel universe to our own. While it appears to be mathematically feasible, there is of course no physical evidence to support the existences of such universes.
But this is not to say that time travel, at least in a limited sense, is not real. When travelling at great speed, or perhaps falling into a black hole, the passage of time does slow down relative to that experienced by stationary observers.
Clocks flown quickly around the world have demonstrated this, displaying time lags in accordance with Einstein’s theory of special relativity.
The 2014 movie Interstellar played on this effect around a black hole, thereby creating a sense of travelling forward in time for astronaut Cooper (played by Matthew McConaughey).
Despite the strangely endearing name, the phrase “black hole” is perhaps somewhat misleading. It implies a hole in space-time through which matter will fall, as opposed to matter falling onto an incredibly dense object.
What actually exists within a black hole’s event horizon is hotly debated. Attempts to understand this include the “fuzzball” picture from string theory, or descriptions of black holes in quantum gravity theories known as “spin foam networks” or “loop quantum gravity”.
One thing that does seem certain is that black holes will continue to intrigue and fascinate us for some time yet.
Source: The Conversation
Știm deja că unele găuri negre au doar de câteva ori masa Soarelui nostru, în timp ce altele sunt mai mult de un miliard de ori mai masive. Dar altele, cu mase intermediare, cum ar fi cea de 2.200 de ori masa Soarelui nostru descoperită recent în star cluster 47 Tucanae, sunt surprinzător de înșelătoare.
Deci, ce este cu aceste închisori gravitaționale care agață ceva ce se apropie prea mult de ele și captează imaginația oamenilor de toate vârstele și profesiile?
„DARK STARS”
Încă din 1783, în cadrul dinamicii newtoniene, conceptul de „stele întunecate” cu o densitate suficient de mare încât nici măcar lumina nu putea scăpa de atracția lor gravitațională a fost avansat de filozoful și matematicianul englez John Michell.
Aproape imediat după ce Albert Einstein și-a prezentat teoria relativității generale în 1915, care a înlocuit descrierea lui Newton despre Universul nostru și a dezvăluit cum spațiul și timpul sunt strâns legate, colegul german Karl Schwarzschild și olandezul Johannes Droste au derivat independent ecuațiile noi pentru o masă sferică sau punctuală .
Deși în momentul în care problema era încă o curiozitate matematică, în ultimul sfert de secol, fizicienii nucleari și-au dat seama că stelele suficient de masive s-ar prăbuși sub propria greutate pentru a deveni aceste găuri negre teoretizate anterior.
Existența lor a fost confirmată în cele din urmă de astronomii care folosesc telescoape puternice, iar mai recent găurile negre care se ciocnesc au fost sursa undelor gravitaționale detectate cu instrumentația LIGO din Statele Unite.
OBIECTUL DENS
Densitățile acestor obiecte sunt uluitoare. Dacă Soarele nostru ar deveni o gaură neagră, va trebui să se prăbușească de la mărimea sa actuală de 1,4 milioane km către o rază mai mică de 3 km (6 km în diametru). Densitatea medie în această “Schwarzschild radius” ar fi de aproape 20 de miliarde de tone pe centimetru cub.
Creșterea forței și atracției gravitaționale pe măsură ce vă apropiați de o gaură neagră poate fi dramatică.
Pe Pământ, forța atracției gravitaționale care vă ține pe suprafața sa este aproximativ aceeași atât picioarele voastre, cât și la nivelul capul, care este puțin mai departe de planetă.
Dar, în apropierea unor găuri negre, diferența de tracțiune gravitațională de la cap până la picioare este atât de mare încât veți fi sfâșiat și întins la nivel atomic, într-un proces numit spaghettificare.
În 1958, fizicianul american David Finkelstein a fost primul care a realizat adevărata natură a ceea ce a ajuns să fie numit „orizontul evenimentului” unei găuri negre. El a descris această limită în jurul unei găuri negre ca o membrană perfectă unidirecțională.
Este o suprafață intangibilă ce încapsulează o sferă fără întoarcere. Odată ajuns în această sferă, tragerea gravitațională a găurii negre este prea mare pentru a scăpa – chiar și pentru lumină.
În 1963, matematicianul din Noua Zeelandă Roy Kerr a rezolvat ecuații mai realiste pentru găurile negre rotative. Acestea au generat curbe de timp închise, care ar permite mișcarea înapoi în timp.
Deși astfel de soluții ciudate pentru ecuațiile relativității generale au apărut pentru prima oară în lucrarea din 1949 a logicianului austro-american Kurt Gödel, se crede că ele trebuie să fie un artefact matematic care încă nu este explicat.
Găură neagră și albă
În 1964, doi americani, scriitorul Ann Ewing și fizicianul teoretic John Wheeler, au introdus termenul „gaura neagră”. Ulterior, în 1965, astrofizicianul teoretic rus Igor Novikov a introdus termenul „gaură albă” pentru a descrie opusul ipotetic al unei găuri negre.
Argumentul a fost că, dacă materia cade într-o gaură neagră, atunci poate că este aruncată în universul nostru dintr-o gaură albă.
Această idee este parțial înrădăcinată în conceptul matematic cunoscut sub numele de pod Einstein-Rosen. Descoperit (matematic) în 1916 de către fizicianul austriac Ludwig Flamm și reintrodus în 1935 de Einstein și de fizicianul american-israelian Nathan Rosen, a fost mai târziu numit „gaură de vierme” de către Wheeler.
În 1962, Wheeler și fizicianul american Robert Fuller au explicat de ce astfel de găuri de vierme ar fi instabile pentru a transporta chiar un singur foton în același univers.
Fapte și ficțiune
Nu este surprinzător că ideea de a intra într-un portal (gaura neagră) și de a se reapărea în altă parte a universului – în spațiu și / sau în timp – a dat naștere unor nenumărate povești science-fiction, printre care Doctor Who, Stargate, Fringe, Farscape and Disney’s Black Hole.
Producțiile în curs de desfășurare pot pur și simplu susține că personajele lor călătoresc într-un univers diferit sau paralel cu al nostru. Deși pare a fi posibil din punct de vedere matematic, nu există desigur dovezi fizice care să susțină existența unor astfel de universuri.
Dar aceasta nu înseamnă că a călători în timp, cel puțin într-un sens limitat, nu poate fi real. Când călătoriți cu mare viteză sau poate cădeați într-o gaură neagră, trecerea timpului încetinește în raport cu cea a observatorilor staționari.
Ceasurile care au zburat repede în întreaga lume au demonstrat acest lucru, prezentând întârzieri în timp, în conformitate cu teoria relativității speciale a lui Einstein.
Filmul Interstellar din 2014 s-a jucat cu acest efect din ptoximitatea unei găuri negre, creând astfel un sentiment de călătorie înainte în timp pentru astronautul Cooper (jucat de Matthew McConaughey).
În ciuda numelui ciudat de ciudat, expresia „gaura neagră” este poate oarecum înșelătoare. Aceasta implică o gaură în spațiu-timp prin care materia va cădea, spre deosebire de materia care cade pe un obiect incredibil de dens.
Ceea ce există de fapt într-un orizont al evenimentului unei găuri negre este dezbătut cu hotărâre. Încercările de a înțelege acest lucru includ imaginea “fuzzball” din teoria corzilor sau descrierile găurilor negre din teoriile gravitației cuantice cunoscute ca “spin foam networks” sau „gravitație cuantică de buclă”.
Un lucru care pare sigur este că găurile negre vor continua să ne intrige și să ne fascineze încă mult timp.
Sursa: The Conversation
Ultima știre din mahala
| VREMEA |
| Bârlad, ora 11:00 | |
| Temperatura | 18.9 °C |
| Umiditatea | 83% |
| Presiunea | 988.7 |
| Vânt | 6.0 m/s |
plouă mocănește și eu am astenie de primăvară 😉


